How Open Source, Open Data and the Cloud are Reshaping Finance Education and the Financial Industry¶
About Me — The Python Quant

Our Vision¶
To revolutionize financial education, research and practice through Python.
Overview & Agenda¶
Today's talk covers the following topics:
- Data Science & Finance Today
- Open Data Science & The Cloud
- The Importance of the Python Ecosystem
- Why Python for Finance?
- How to Learn and Do Python for Finance?
- A "Complete Package" Example
Data Science & Finance Today¶
Data Science Defined¶
For instance, Wikipedia defines the field as follows (cf. https://en.wikipedia.org/wiki/Data_science):
Data science is an interdisciplinary field about processes and systems to extract knowledge or insights from data in various forms, either structured or unstructured, which is a continuation of some of the data analysis fields such as statistics, data mining, and predictive analytics, ...
Explosion in Data¶
Real-Time Economy & High Frequency¶
Established Tools Cannot Cope¶
"Big data is data that does not fit into an Excel spreadsheet." Unknown.

Traditional (IT) Processes Inappropriate¶
“If I had asked people what they wanted, they would have said faster horses.” Henry Ford
The Rise of Open Data Science¶
Open Source as the New Standard¶
Open (Financial) Data Up and Coming¶
Open Communities Replace Old Networks¶
The Browser as Operating System¶
Cloud Storage Going Corporate¶
Unlimited, Affordable Compute Power¶
The Importance of the Python Ecosystem Today¶
In Education¶
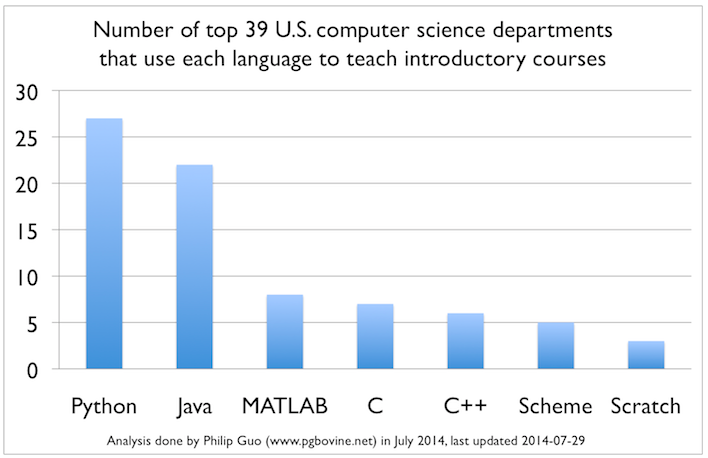
Data Science Languages¶
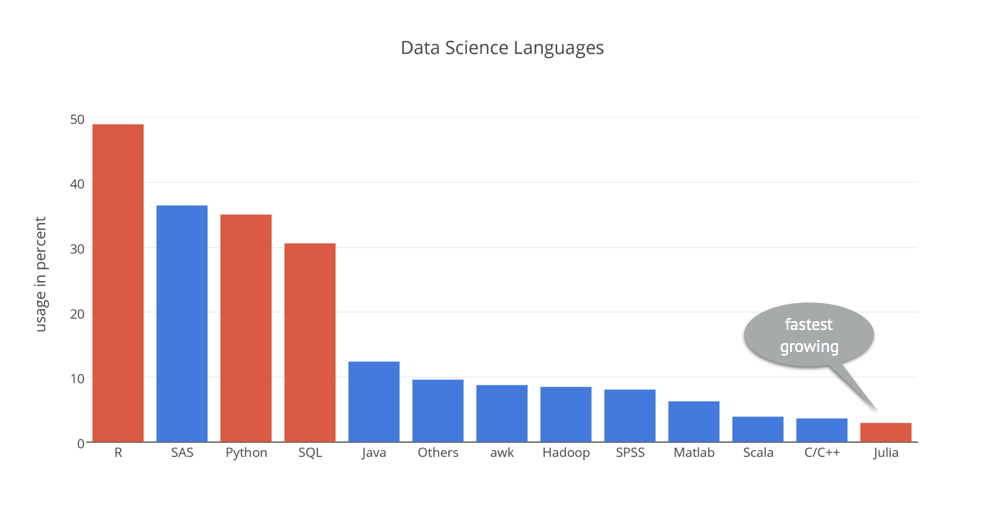
Source: http://kdnuggets.com
Programming Languages in General¶
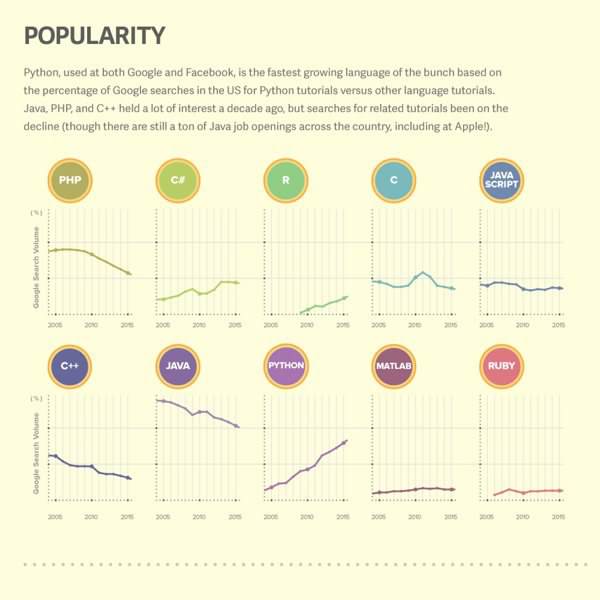
Source: http://boingboing.net
Technology Giants¶

Financial Giants¶
Why Python for Finance?¶
Financial Algorithm Example¶
In Python, you generally start with the import of some libraries and packages.
from pandas import *
from pylab import *
from pandas_datareader import data as web
from seaborn import *; set()
%matplotlib inline
Consider the stochastic differential equation of a geometric Brownian motion as used by Black-Scholes-Merton (1973), describing the evolution of a stock index over time, for example.
$$ dS_t = rS_td_t+ \sigma S_tdZ_t $$A possible Euler discretization to simulate the time $T$ value of $S$ is given by the difference equation
$$ S_T = S_0 e^{ \left( r - \frac{\sigma^2}{2} \right) T + \sigma \sqrt{T} z } $$with $z$ being a standard normally distributed random variable.
The simulation of 10,000,000 time $T$ values for the index with Python is efficient and fast, the syntax is really concise.
%%time
S0 = 100.; r = 0.05; sigma = 0.2; T = 1.
z = standard_normal(10000000)
ST = S0 * exp((r - 0.5 * sigma ** 2) * T + sigma * sqrt(T) * z)
CPU times: user 787 ms, sys: 165 ms, total: 952 ms Wall time: 1.33 s
We would expect for the mean value $\bar{S}_T = S_0 \cdot e^{r T} \approx 105.1$.
S0 * exp(r * T)
105.12710963760242
ST.mean()
105.135621517714
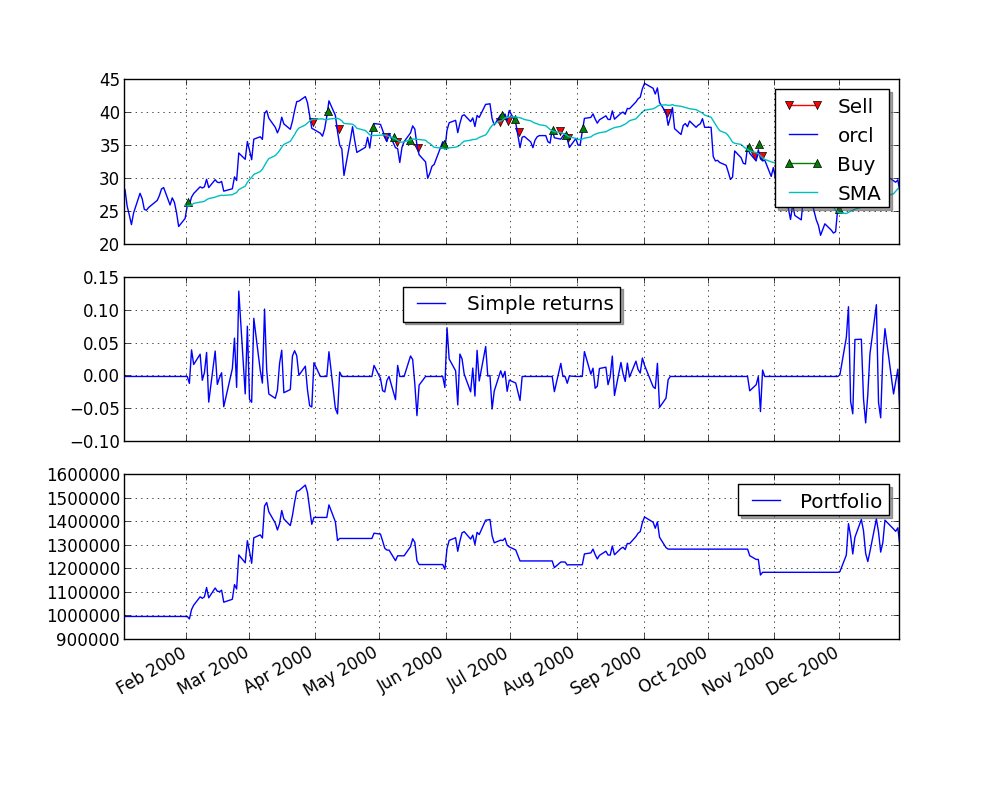
The histogram of the simulated values with mean value (red line).
figure(figsize=(10, 6))
hist(ST, bins=45);
axvline(ST.mean(), color='r');
In addition, option pricing by Monte Carlo simulation is also easily implemented.
%%time
strike = 105. # option strike
payoff = maximum(ST - strike, 0) # payoff at maturity
C0 = exp(-r * T) * payoff.mean() # MCS estimator
print 'Europen call option value is %.2f.' % C0
Europen call option value is 8.02. CPU times: user 151 ms, sys: 57.7 ms, total: 209 ms Wall time: 333 ms
Financial Data Science Example¶
We read historical daily closing data for the S&P 500 index.
spx = web.DataReader('^GSPC', data_source='yahoo')['Close']
spx.tail()
Date 2016-06-14 2075.320068 2016-06-15 2071.500000 2016-06-16 2077.989990 2016-06-17 2071.219971 2016-06-20 2083.250000 Name: Close, dtype: float64
A simple method call allows us to visualize the time series data.
spx.plot(figsize=(10, 6));
We also read historical closing data for the VIX volatility index ...
vix = web.DataReader('^VIX', data_source='yahoo')['Close']
vix.tail()
Date 2016-06-14 20.500000 2016-06-15 20.139999 2016-06-16 19.370001 2016-06-17 19.410000 2016-06-20 18.370001 Name: Close, dtype: float64
... and visualize it.
vix.plot(figsize=(10, 6));
First, we combine the two data sets into one.
data = DataFrame({'SPX': spx, 'VIX': vix})
data.tail()
| SPX | VIX | |
|---|---|---|
| Date | ||
| 2016-06-14 | 2075.320068 | 20.500000 |
| 2016-06-15 | 2071.500000 | 20.139999 |
| 2016-06-16 | 2077.989990 | 19.370001 |
| 2016-06-17 | 2071.219971 | 19.410000 |
| 2016-06-20 | 2083.250000 | 18.370001 |
Second, let us plot the data into a single diagram.
data.plot(figsize=(10, 6), secondary_y='VIX', title='');
Let us calculate the log returns for the two time series. This task is accomplished by a highly vectorized operation ("no looping").
rets = log(data / data.shift(1))
rets.head()
| SPX | VIX | |
|---|---|---|
| Date | ||
| 2010-01-04 | NaN | NaN |
| 2010-01-05 | 0.003111 | -0.035038 |
| 2010-01-06 | 0.000545 | -0.009868 |
| 2010-01-07 | 0.003993 | -0.005233 |
| 2010-01-08 | 0.002878 | -0.050024 |
Now we can, for instance, calculate the correlation between the two time series.
rets.corr()
| SPX | VIX | |
|---|---|---|
| SPX | 1.000000 | -0.828457 |
| VIX | -0.828457 | 1.000000 |
"Use a picture. It's worth a thousand words." Tass Flanders (1911)
jointplot(rets['SPX'], rets['VIX'], kind='reg', size=7);
How to Learn and Do Python for Finance?¶
Python Books¶
Python Training¶
Python Conferences¶

Saturday here in Singapore at PyCon as well ...
For Python Quants Series¶
Online & Corporate Training¶
University Degrees¶
1st Python For Finance University Certificate¶
Master of Science Degree¶

Currently in the planning phase:
Master of Science in Financial Data Science and Computational Finance
Python-based Financial Research¶
Open Communities¶
Open Source Libraries¶
PyThalesians¶
PyAlgoTrade¶
zipline¶
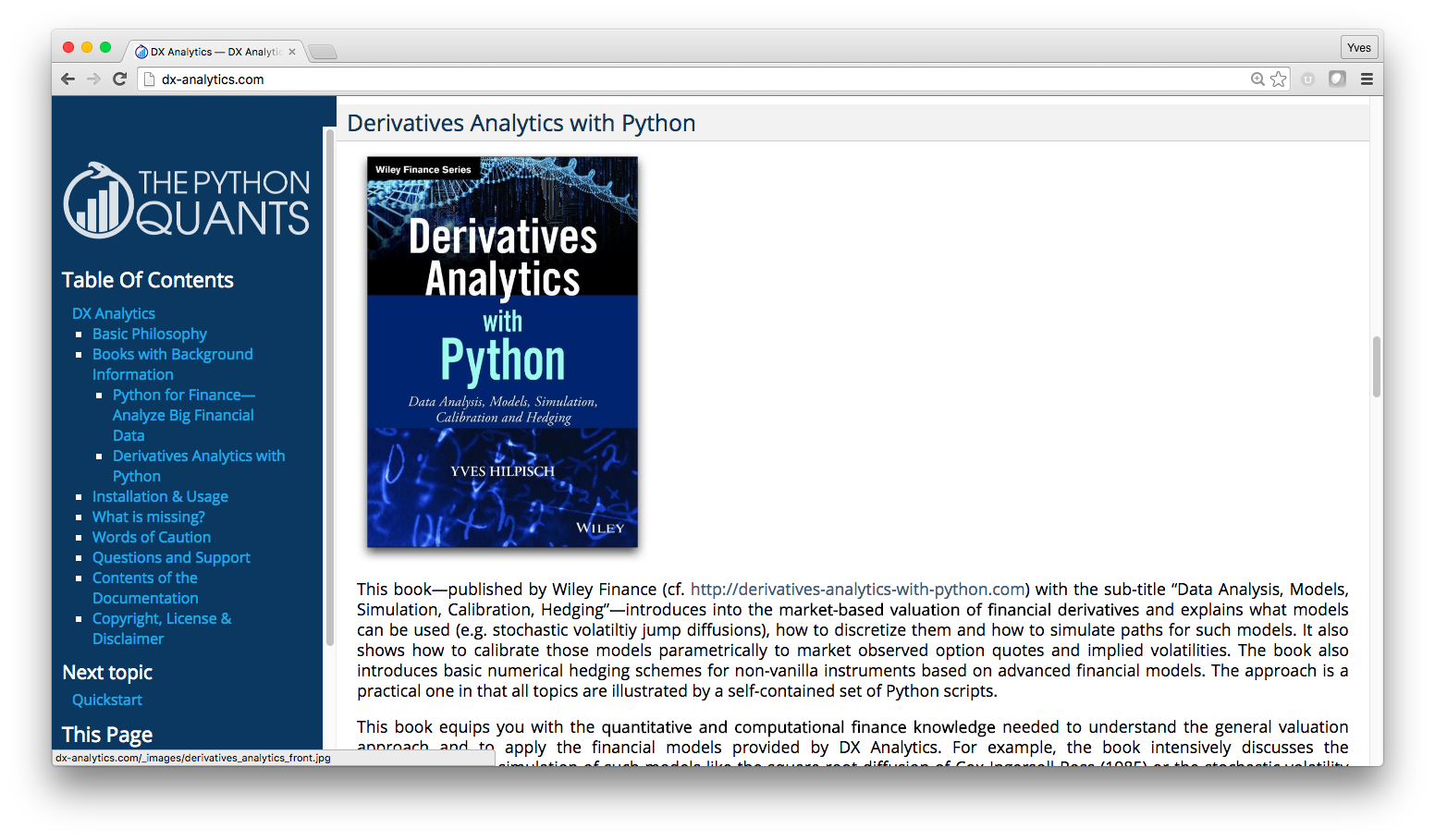
DX Analytics¶
Platforms¶
Quantopian¶
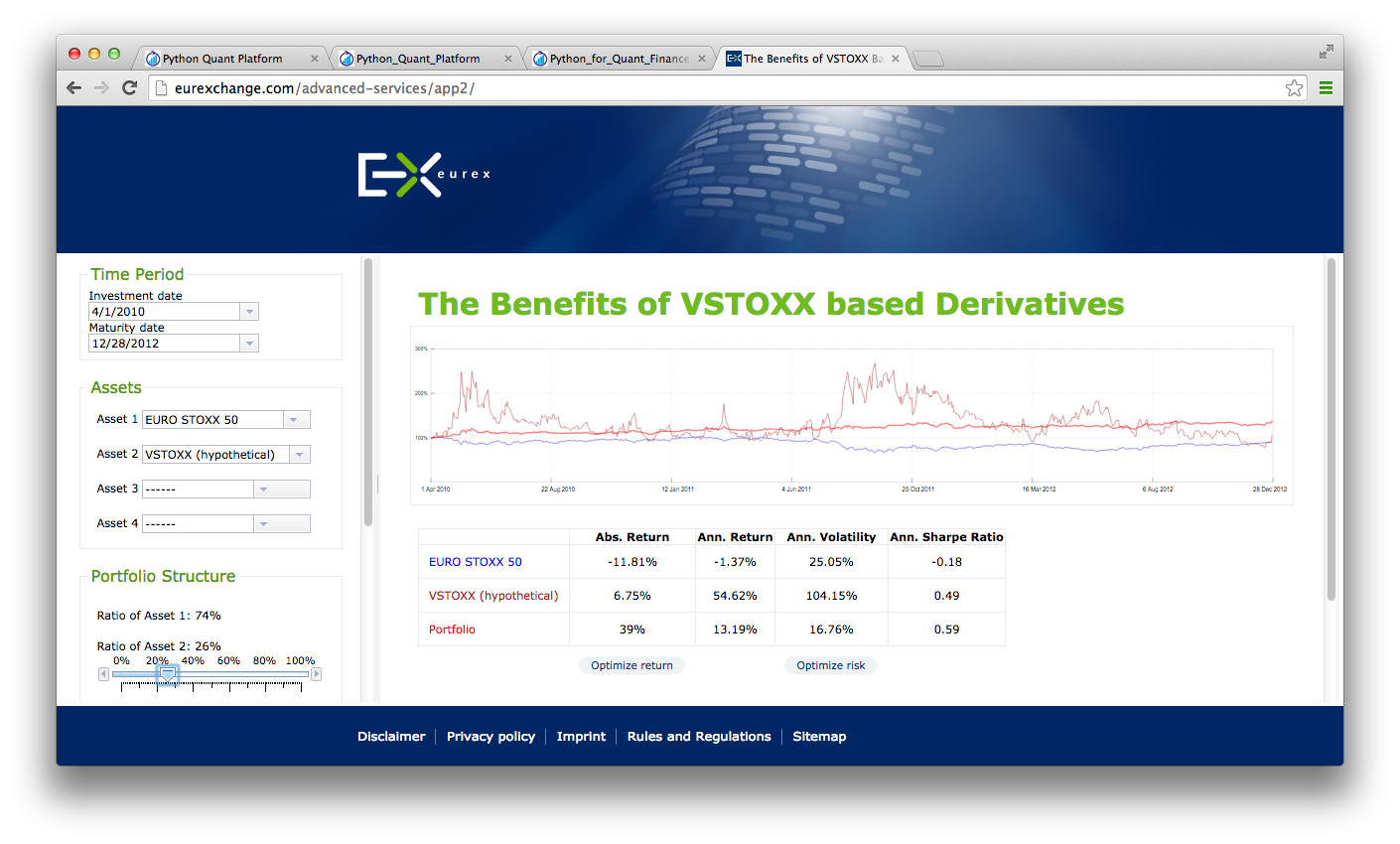
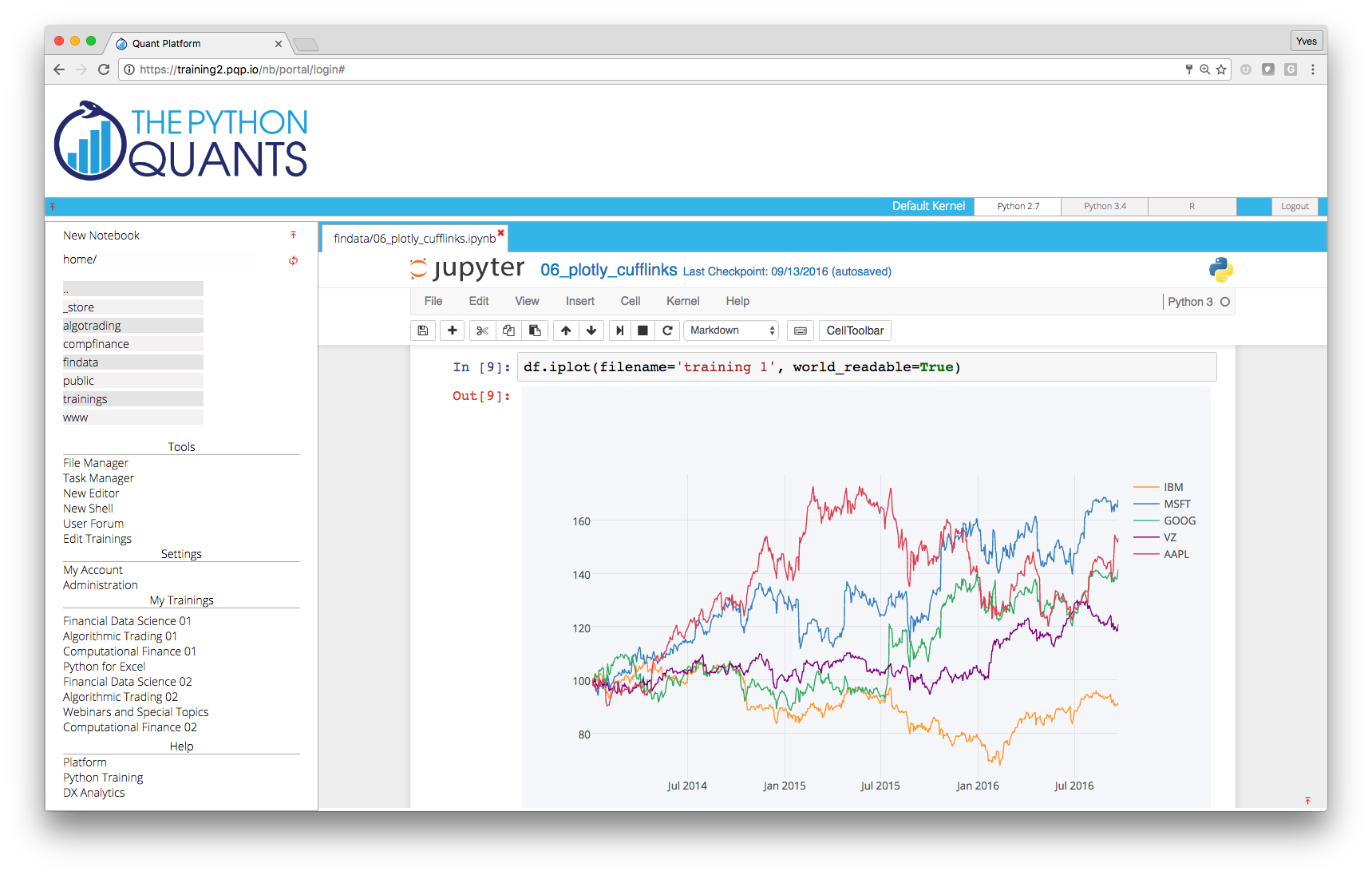
Quant Platform¶
Beacon¶
A "Complete Package" Example¶
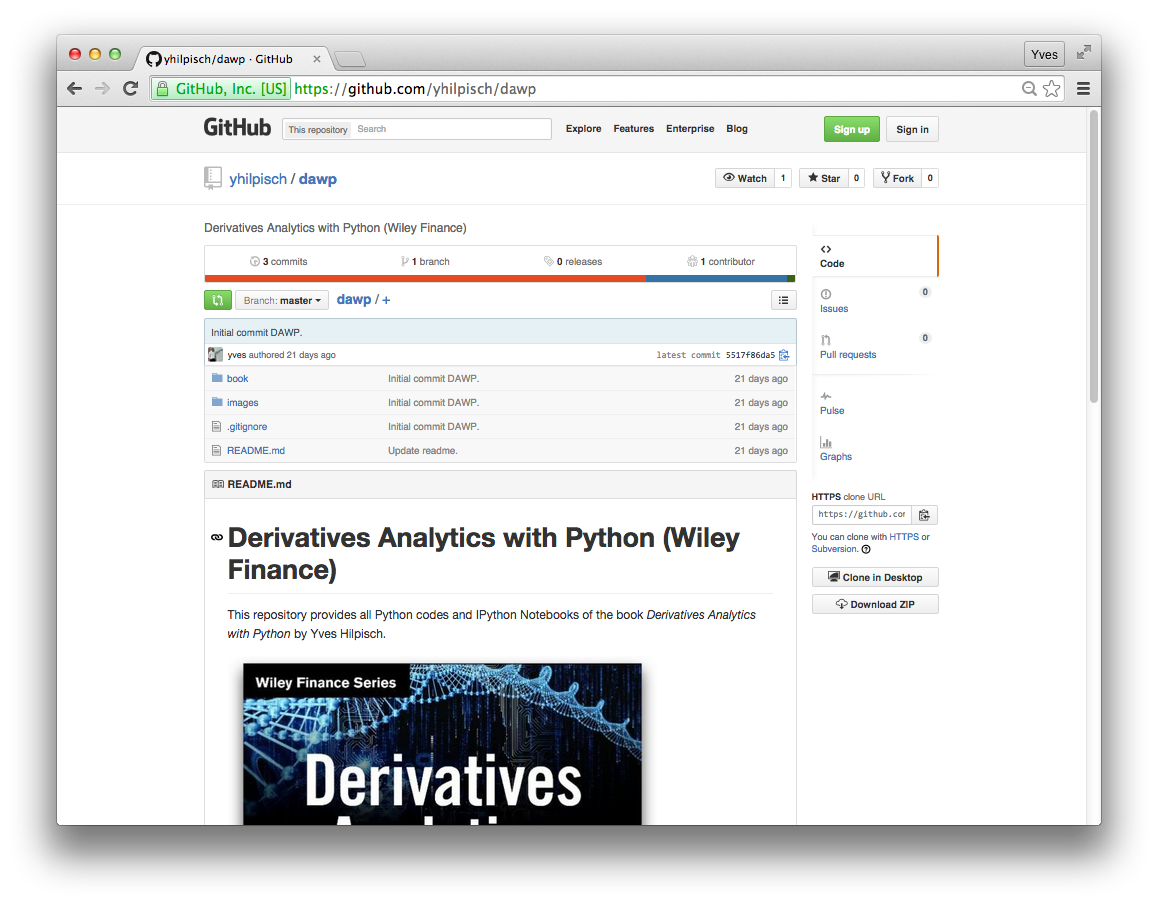
Derivatives Analytics with Python
Book¶
Github Repository¶
Code Hosting¶
DX Analytics as Library also Hosted¶
Online Training¶
Python for Finance¶
Python has become the English of programming languages (for finance).
If you have only time to learn one programming language for finance (thoroughly), learn Python.

http://tpq.io | @dyjh | team@tpq.io
Python Quant Platform | http://quant-platform.com
Python for Finance | Python for Finance @ O'Reilly
Derivatives Analytics with Python | Derivatives Analytics @ Wiley Finance
Listed Volatility and Variance Derivatives | Listed VV Derivatives @ Wiley Finance