The Python Quants

Data Science with Python

htw saar

Saarbrücken, 01. June 2016

Dr. Yves J. Hilpisch

About Me & TPQ

The Python Quant

http://tpq.io

http://eurexchange.com/advanced-services/

Technology

http://datapark.io

http://dx-analytics.com

Author

http://pff.tpq.io

http://dawp.tpq.io

http://lvvd.tpq.io

Trainer, Lecturer & Speaker

http://training.tpq.io

For the curious:

Quick Overview

Today's talk covers the following topics:

  • Data Science
  • Python
    • Data Structures
    • Simple Algorithms
    • Financial Algorithm Example
    • Financial Data Science Example
  • Case Study
  • Outlook

Data Science

Data Science Defined

For instance, Wikipedia defines the field as follows (cf. https://en.wikipedia.org/wiki/Data_science):

Data science is an interdisciplinary field about processes and systems to extract knowledge or insights from data in various forms, either structured or unstructured, which is a continuation of some of the data analysis fields such as statistics, data mining, and predictive analytics, ...

Explosion in Data

Source: http://www.umuc.edu/analytics/about/big-data-job-growth-infographic.cfm

Real-Time Economy & High Frequency

Source: http://www.qfac.ca/high-frequency-trading-an-evolving-exchange/

Established Tools Cannot Cope

"Big data is data that does not fit into an Excel spreadsheet." Unknown.

Traditional (IT) Processes Inappropriate

“If I had asked people what they wanted, they would have said faster horses.” Henry Ford

The Rise of Open Data Science

Open Source as the New Standard

http://github.com

Open (Financial) Data Up and Coming

http://quandl.com

Open Communities Replace Old Networks

http://meetup.com

The Browser as Operating System

http://jupyter.org

Cloud Storage Going Corporate

http://dropbox.com

Unlimited, Affordable Compute Power

http://digitalocean.com

Python

Data Structures

Linus Torvalds:

Bad programmers worry about the code. Good programmers worry about data structures and their relationships.

Artihmetic operations on numerical data types (I).

In [1]:
3 + 4
Out[1]:
7
In [2]:
x = 2
3 * x ** 2 + 5
Out[2]:
17
In [3]:
type(x)
Out[3]:
int

Artihmetic operations on numerical data types (II).

In [4]:
a = 3 * 1.5
a
Out[4]:
4.5
In [5]:
type(3)
Out[5]:
int
In [6]:
type(1.5)
Out[6]:
float
In [7]:
type(a)
Out[7]:
float

String objects are iterable sequences.

In [8]:
s = 'This is Python.'
In [9]:
for c in s:
    print c,

T h i s   i s   P y t h o n .
In [10]:
s[2:4]  # zero-based numbering/indexing
Out[10]:
'is'
In [11]:
s.find('Python')
Out[11]:
8

Python data (object) model allows for a unified interaction of objects with standard Python operators (instructions).

In [12]:
2 * s
Out[12]:
'This is Python.This is Python.'
In [13]:
s[:8] + s[9:].capitalize()
Out[13]:
'This is Ython.'

List objects are mutable, ordered sequences of other objects.

In [14]:
l = [2, 1.5, 'Python']
In [15]:
l.append('htw saar')
l
Out[15]:
[2, 1.5, 'Python', 'htw saar']
In [16]:
range(2, 20, 2)  # start, end, step size
Out[16]:
[2, 4, 6, 8, 10, 12, 14, 16, 18]

Dictionary objects are mutable, unordered, hashable key-value stores.

In [17]:
d = {'a': 1, 'b': [2, 2.5], 'c': 'Python'}
In [18]:
d
Out[18]:
{'a': 1, 'b': [2, 2.5], 'c': 'Python'}
In [19]:
d['b']  # data access via key
Out[19]:
[2, 2.5]
In [20]:
d['c']
Out[20]:
'Python'

The NumPy library is designed to handle multi-dimensional numerical data structures.

In [21]:
import numpy as np
In [22]:
a = np.random.standard_normal((3, 5))
a
Out[22]:
array([[ 0.88458232,  0.51438722,  1.40373974, -0.20738244,  0.82008834],
       [-0.48297603, -1.3426828 ,  1.48195138,  0.19109117,  0.41994271],
       [-1.55576775, -0.23579534, -2.05921299, -0.35005397, -0.44885767]])
In [23]:
a.mean()
Out[23]:
-0.064463074534616277
In [24]:
a.std()
Out[24]:
1.0051957622433556

Simple Algorithms

Let us implement a binary search algorithm first. This algorithm searches for an element in an ordered list, starts in the middle and goes then up or down, restarting in the middle, etc. In our case it returns True if successful and False if not.

In [25]:
def binary_search(li, e):
    f = 0
    l = len(li)
    if e < li[0] or e > li[-1]:
        return False
    while f < l:
        m = (l + f) // 2
        # print f, l, m, li[m]
        if li[m] == e:
            return True
        if e > li[m]:
            f = m
        else:
            l = m
    return False

And the application to a numerical data set.

In [26]:
N = 100
a = range(N)
print a

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99]
In [27]:
binary_search(a, 95)
Out[27]:
True
In [28]:
binary_search(a, 105)
Out[28]:
False
In [29]:
binary_search(a, 0)
Out[29]:
True

Another ordered sequence (i.e. string object) on which we can do the search.

In [30]:
import string
a = string.lowercase
a
Out[30]:
'abcdefghijklmnopqrstuvwxyz'
In [31]:
binary_search(a, 'y')
Out[31]:
True
In [32]:
binary_search(a, 'l')
Out[32]:
True
In [33]:
binary_search(a, 'B')
Out[33]:
False

Prime Characteristic of Integer

The following function decides whether a given integer is a prime or not.

In [34]:
def is_prime(I):
    end = int(I ** 0.5) + 1
    if I % 2 == 0:
        return False
    for i in xrange(3, end, 2):
        if I % i == 0:
            return False
    return True

A couple of examples.

In [35]:
is_prime(7)
Out[35]:
True
In [36]:
is_prime(100)
Out[36]:
False
In [37]:
%time is_prime(100000007)

CPU times: user 715 µs, sys: 620 µs, total: 1.34 ms
Wall time: 804 µs
Out[37]:
True
In [38]:
p = 100109100129162907  # larger prime
%time is_prime(p)

CPU times: user 10.4 s, sys: 10.2 ms, total: 10.4 s
Wall time: 10.4 s
Out[38]:
True

Python can handle quite/arbitrarily large integers.

In [39]:
p.bit_length()
Out[39]:
57
In [40]:
g = 10 ** 100  # googol number
g
Out[40]:
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000L
In [41]:
g.bit_length()
Out[41]:
333

Financial Algorithm Example

In Python, you generally start with the import of some libraries and packages.

In [42]:
from pandas import *
from pylab import *
from pandas_datareader import data as web
from seaborn import *; set()
%matplotlib inline

Consider the stochastic differential equation of a geometric Brownian motion as used by Black-Scholes-Merton (1973), describing the evolution of a stock index over time, for example.

$$ dS_t = rS_td_t+ \sigma S_tdZ_t $$

A possible Euler discretization to simulate the time $T$ value of $S$ is given by the difference equation

$$ S_T = S_0 e^{ \left( r - \frac{\sigma^2}{2} \right) T + \sigma \sqrt{T} z } $$

with $z$ being a standard normally distributed random variable.

The simulation of 10,000,000 time $T$ values for the index with Python is efficient and fast, the syntax is really concise.

In [43]:
%%time
S0 = 100.; r = 0.05; sigma = 0.2; T = 1.
z = standard_normal(10000000)
ST = S0 * exp((r - 0.5 * sigma ** 2) * T + sigma * sqrt(T) * z)

CPU times: user 432 ms, sys: 87.2 ms, total: 519 ms
Wall time: 518 ms

We would expect for the mean value $\bar{S}_T = S_0 \cdot e^{r T} \approx 105.1$.

In [44]:
S0 * exp(r  * T)
Out[44]:
105.12710963760242
In [45]:
ST.mean()
Out[45]:
105.12649538700849

The histogram of the simulated values with mean value (red line).

In [46]:
figure(figsize=(10, 6))
hist(ST, bins=45);
axvline(ST.mean(), color='r');

In addition, option pricing by Monte Carlo simulation is also easily implemented.

In [47]:
strike = 105.  # option strike
payoff = maximum(ST - strike, 0)  # payoff at maturity
C0 = exp(-r * T) * payoff.mean()  # MCS estimator
print 'Europen call option value is %.2f.' % C0

Europen call option value is 8.02.

Financial Data Science Example

We read historical daily closing data for the S&P 500 index.

In [48]:
spx = web.DataReader('^GSPC', data_source='yahoo')['Close']
In [49]:
spx.tail()
Out[49]:
Date
2016-05-23    2048.040039
2016-05-24    2076.060059
2016-05-25    2090.540039
2016-05-26    2090.100098
2016-05-27    2099.060059
Name: Close, dtype: float64

A simple method call allows us to visualize the time series data.

In [50]:
spx.plot(figsize=(10, 6));

We also read historical closing data for the VIX volatility index ...

In [51]:
vix = web.DataReader('^VIX', data_source='yahoo')['Close']
In [52]:
vix.tail()
Out[52]:
Date
2016-05-23    15.82
2016-05-24    14.42
2016-05-25    13.90
2016-05-26    13.43
2016-05-27    13.12
Name: Close, dtype: float64

... and visualize it.

In [53]:
vix.plot(figsize=(10, 6));

First, we combine the two data sets into one.

In [54]:
data = DataFrame({'SPX': spx, 'VIX': vix})
In [55]:
data.tail()
Out[55]:
SPX VIX
Date
2016-05-23 2048.040039 15.82
2016-05-24 2076.060059 14.42
2016-05-25 2090.540039 13.90
2016-05-26 2090.100098 13.43
2016-05-27 2099.060059 13.12

Let us calculate the log returns for the two time series. This task is accomplished by a highly vectorized operation ("no looping").

In [56]:
rets = log(data / data.shift(1))
In [57]:
rets.tail()
Out[57]:
SPX VIX
Date
2016-05-23 -0.002088 0.039980
2016-05-24 0.013589 -0.092659
2016-05-25 0.006951 -0.036727
2016-05-26 -0.000210 -0.034398
2016-05-27 0.004278 -0.023353

Now we can, for instance, calculate the correlation between the two time series.

In [58]:
rets.corr()
Out[58]:
SPX VIX
SPX 1.000000 -0.829904
VIX -0.829904 1.000000

"Use a picture. It's worth a thousand words." Tass Flanders (1911)

In [59]:
jointplot(rets['SPX'], rets['VIX'], kind='reg', size=7);

Case Study — Titanic Survivors

We work with a data set as provided on the Web page https://vincentarelbundock.github.io/Rdatasets/datasets.html.

Let us have a look at the raw data which is stored as a comma separated value (CSV) file.

In [60]:
with open('Titanic.csv', 'r') as f:
    for _ in range(10):
        print f.readline(),

"","Class","Sex","Age","Survived","Freq"
"1","1st","Male","Child","No",0
"2","2nd","Male","Child","No",0
"3","3rd","Male","Child","No",35
"4","Crew","Male","Child","No",0
"5","1st","Female","Child","No",0
"6","2nd","Female","Child","No",0
"7","3rd","Female","Child","No",17
"8","Crew","Female","Child","No",0
"9","1st","Male","Adult","No",118

We read the data with the pandas data analytics library.

In [61]:
data = pd.read_csv('Titanic.csv', index_col=0)
In [62]:
data.tail()
Out[62]:
Class Sex Age Survived Freq
28 Crew Male Adult Yes 192
29 1st Female Adult Yes 140
30 2nd Female Adult Yes 80
31 3rd Female Adult Yes 76
32 Crew Female Adult Yes 20
In [63]:
len(data)  # len of data set = number of groups
Out[63]:
32

The data can now be analyzed in several dimensions. Let us see what difference the sex makes. First, the total number of passengers by sex.

In [64]:
grouped = data.groupby('Sex')
In [65]:
grouped.sum()
Out[65]:
Freq
Sex
Female 470
Male 1731

Second, the the survivors vs. those that did not.

In [66]:
grouped = data.groupby(['Sex', 'Survived'])
In [67]:
grouped.sum()
Out[67]:
Freq
Sex Survived
Female No 126
Yes 344
Male No 1364
Yes 367

Next, the class to which the passengers belonged.

In [68]:
grouped = data.groupby('Class')
In [69]:
grouped.sum()
Out[69]:
Freq
Class
1st 325
2nd 285
3rd 706
Crew 885

And the relation between survivors and non-survivors.

In [70]:
grouped = data.groupby(['Class', 'Survived'])
In [71]:
grouped.sum()
Out[71]:
Freq
Class Survived
1st No 122
Yes 203
2nd No 167
Yes 118
3rd No 528
Yes 178
Crew No 673
Yes 212

Finally, the complete overview via grouping.

In [72]:
grouped = data.groupby(['Class', 'Sex', 'Age', 'Survived'])
In [73]:
grouped.sum()
Out[73]:
Freq
Class Sex Age Survived
1st Female Adult No 4
Yes 140
Child No 0
Yes 1
Male Adult No 118
Yes 57
Child No 0
Yes 5
2nd Female Adult No 13
Yes 80
Child No 0
Yes 13
Male Adult No 154
Yes 14
Child No 0
Yes 11
3rd Female Adult No 89
Yes 76
Child No 17
Yes 14
Male Adult No 387
Yes 75
Child No 35
Yes 13
Crew Female Adult No 3
Yes 20
Child No 0
Yes 0
Male Adult No 670
Yes 192
Child No 0
Yes 0

The same analysis with percent values.

In [74]:
perc = grouped.sum() / grouped.sum().sum() * 100
perc
Out[74]:
Freq
Class Sex Age Survived
1st Female Adult No 0.181736
Yes 6.360745
Child No 0.000000
Yes 0.045434
Male Adult No 5.361199
Yes 2.589732
Child No 0.000000
Yes 0.227169
2nd Female Adult No 0.590641
Yes 3.634711
Child No 0.000000
Yes 0.590641
Male Adult No 6.996820
Yes 0.636075
Child No 0.000000
Yes 0.499773
3rd Female Adult No 4.043617
Yes 3.452976
Child No 0.772376
Yes 0.636075
Male Adult No 17.582917
Yes 3.407542
Child No 1.590186
Yes 0.590641
Crew Female Adult No 0.136302
Yes 0.908678
Child No 0.000000
Yes 0.000000
Male Adult No 30.440709
Yes 8.723308
Child No 0.000000
Yes 0.000000

A ranking according to the percent values.

In [75]:
ranking = perc.rank()
ranking
Out[75]:
Freq
Class Sex Age Survived
1st Female Adult No 11.0
Yes 28.0
Child No 4.5
Yes 9.0
Male Adult No 27.0
Yes 22.0
Child No 4.5
Yes 12.0
2nd Female Adult No 15.0
Yes 25.0
Child No 4.5
Yes 15.0
Male Adult No 29.0
Yes 17.5
Child No 4.5
Yes 13.0
3rd Female Adult No 26.0
Yes 24.0
Child No 19.0
Yes 17.5
Male Adult No 31.0
Yes 23.0
Child No 21.0
Yes 15.0
Crew Female Adult No 10.0
Yes 20.0
Child No 4.5
Yes 4.5
Male Adult No 32.0
Yes 30.0
Child No 4.5
Yes 4.5

Finally, the sorted ranking.

In [76]:
ranking.sort_values(by='Freq', ascending=False)
Out[76]:
Freq
Class Sex Age Survived
Crew Male Adult No 32.0
3rd Male Adult No 31.0
Crew Male Adult Yes 30.0
2nd Male Adult No 29.0
1st Female Adult Yes 28.0
Male Adult No 27.0
3rd Female Adult No 26.0
2nd Female Adult Yes 25.0
3rd Female Adult Yes 24.0
Male Adult Yes 23.0
1st Male Adult Yes 22.0
3rd Male Child No 21.0
Crew Female Adult Yes 20.0
3rd Female Child No 19.0
2nd Male Adult Yes 17.5
3rd Female Child Yes 17.5
2nd Female Adult No 15.0
Child Yes 15.0
3rd Male Child Yes 15.0
2nd Male Child Yes 13.0
1st Male Child Yes 12.0
Female Adult No 11.0
Crew Female Adult No 10.0
1st Female Child Yes 9.0
2nd Male Child No 4.5
Female Child No 4.5
1st Male Child No 4.5
Crew Female Child No 4.5
Yes 4.5
1st Female Child No 4.5
Crew Male Child No 4.5
Yes 4.5

The Python Quants

http://tpq.io | @dyjh | team@tpq.io

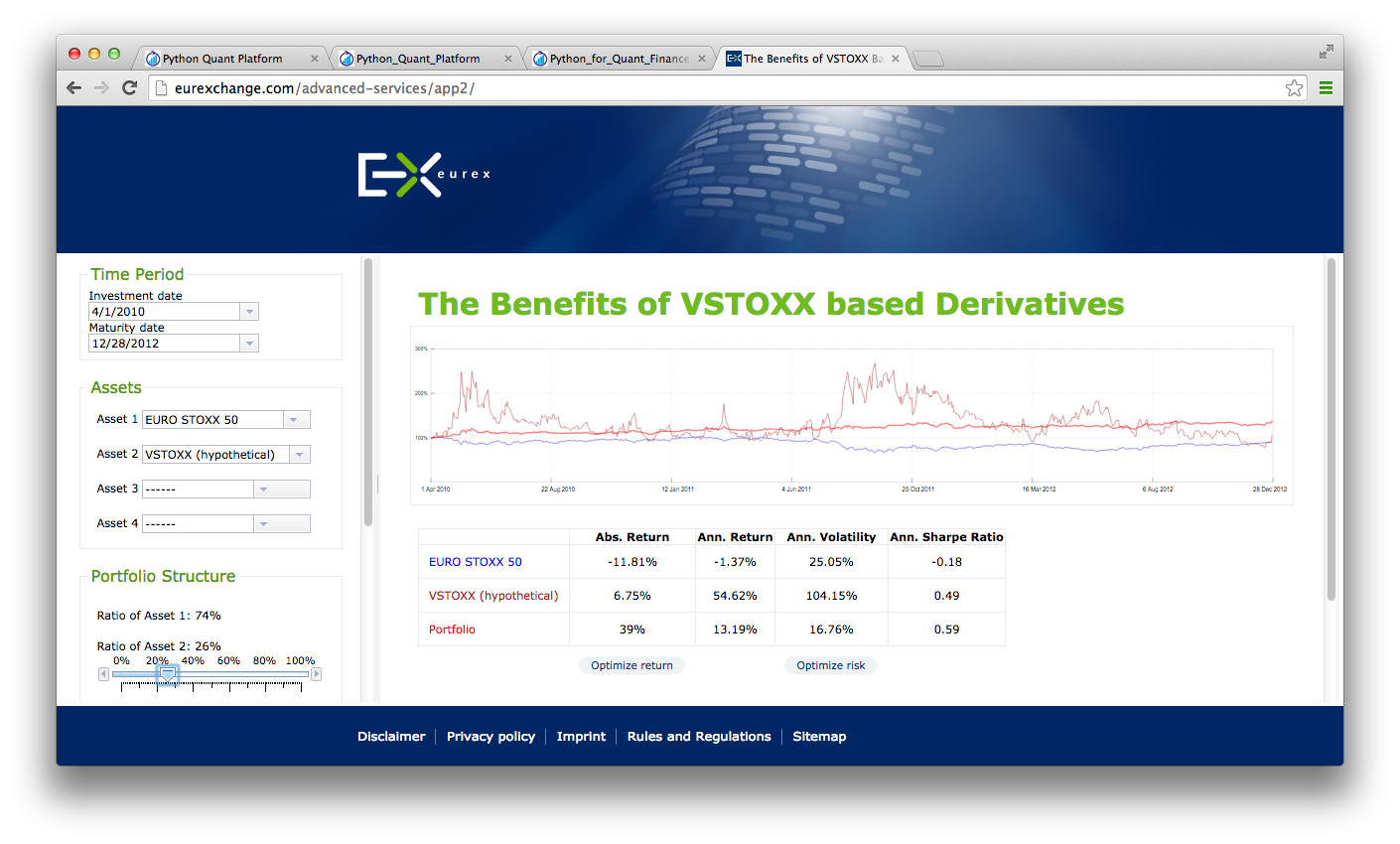
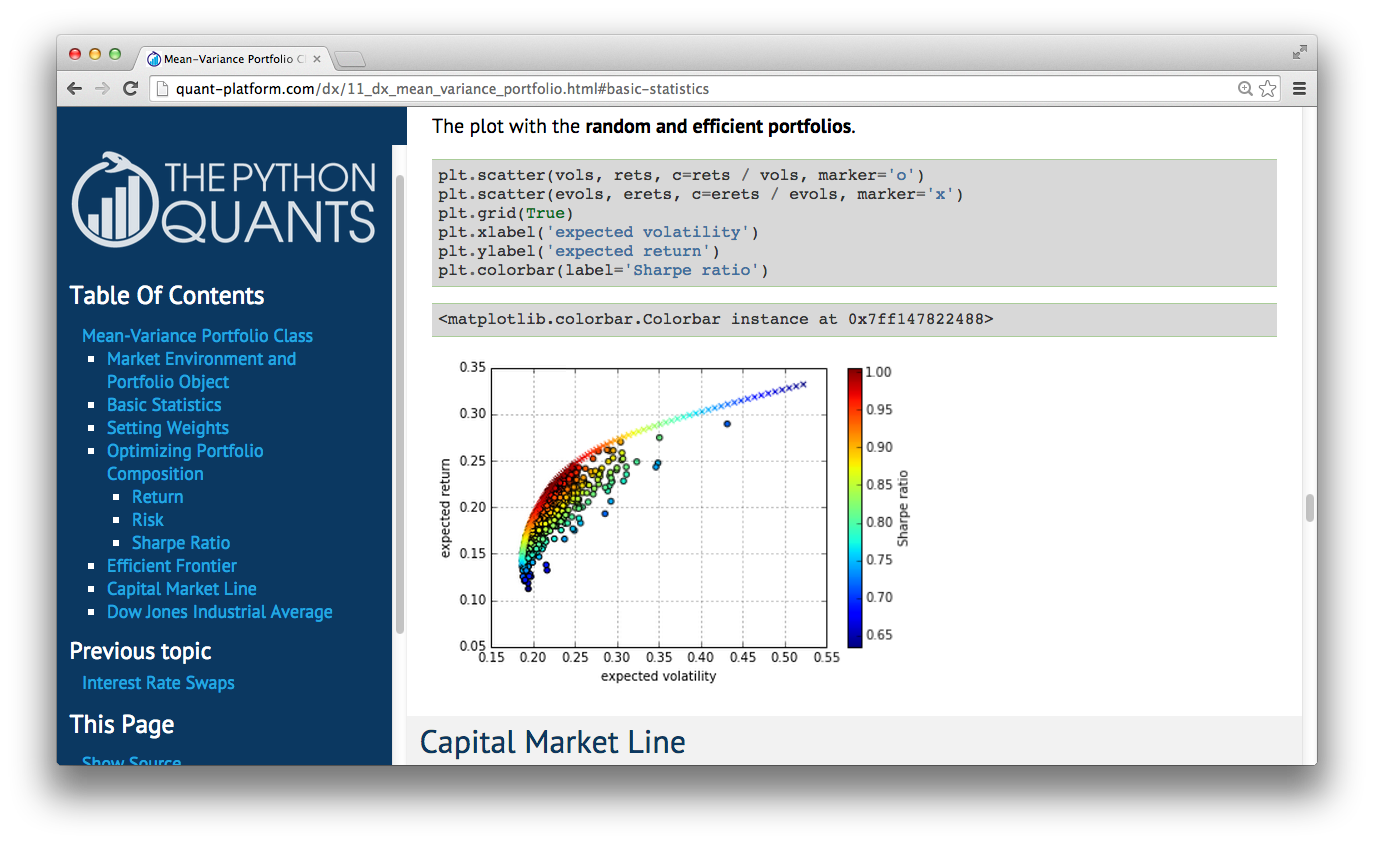
Python Quant Platform | http://quant-platform.com

Python for Finance | Python for Finance @ O'Reilly

Derivatives Analytics with Python | Derivatives Analytics @ Wiley Finance

Listed Volatility and Variance Derivatives | Listed VV Derivatives @ Wiley Finance